
2013 CMS Summer Meeting, Halifax
Interests
- Fractal Geometry
- Fractal Analysis
- Mathematical Physics
- Numerical Methods
- Optimization
- Number Theory
- Connections of the above
Download
- Google Drive — most recent versions of all my papers
- arXiv.org — please use to cite my unpublished papers
Papers on Computational Methods
13. A Computational Resolution of the Inverse Problem of Kinetic Capillary Electrophoresis (KCE)
- 2018, Recent Advances in Mathematical & Statistical Methods, Springer.
- Determining kinetic rate constants is a highly relevant problem in biochemistry, so various methods have been designed to extract them from experimental data. Such methods have two main components: the experimental apparatus and the subsequent analysis, the latter often dependent on mathematical theory. Thus the theoretical approach taken influences the effectiveness of constant determination. A computational inverse problem approach is hereby presented, which does not merely give a single rough approximation of the sought constants, but is inherently capable of determining them from exact signals to arbitrary accuracy. This approach is thus not merely novel, but opens a whole new category of solution approaches in the field, enabled primarily by an efficient direct solver.
12. Estimating Kinetic Rate Constants and Plug Concentration Profiles from Simulated KCE Electropherogram Signals
- Kinetic rate constants fundamentally characterize the dynamics of the chemical interaction of macromolecules, and thus their study sets a major direction in experimental biochemistry. The estimation of such constants is often challenging, partly due to the noisiness of data, and partly due to the theoretical framework. Novel and qualitatively reasonable methods are presented for the estimation of the rate constants of complex formation and dissociation in Kinetic Capillary Electrophoresis (KCE). This also serves the broader effort to resolve the inverse problem of KCE, where these estimates pose as initial starting points in the non-linear optimization space, along with the asymmetric Gaussian parameters describing the injected plug concentration profiles, which is also hereby estimated. This rate constant estimation method is also compared to an earlier one.
11. A Fast Stable Discretization of the Constant-Convection-Diffusion-Reaction Equations of Kinetic Capillary Electrophoresis (KCE)
- 2017, Applied Numerical Mathematics. Vol. 122, Dec. 2017, p. 82-91.
- A discretization scheme is introduced for a set of convection–diffusion equations with a non-linear reaction term, where the convection velocity is constant for each reactant. This constancy allows a transformation to new spatial variables, which ensures the global stability of discretization. Convection–diffusion equations are notorious for their lack of stability, arising from the algebraic interaction of the convection and diffusion terms. Unexpectedly, our implemented numerical algorithm proves to be faster than computing exact solutions derived for a special case, while remaining reasonably accurate, as demonstrated in our runtime and error analysis.
Papers on Fractals
10. On the Exact Convex Hull of IFS Fractals
- 2018, Fractals, Vol. 26, No. 1, 1850002.
- The problem of finding the convex hull of an IFS fractal is relevant in both theoretical and computational settings. Various methods exist that approximate it, but our aim is its exact determination. The finiteness of extremal points is examined a priori from the IFS parameters, revealing some cases when the convex hull problem is solvable. Former results are detailed from the literature, and two new methods are introduced and crystallized for practical applicability — one more general, the other more efficient. Focal periodicity in the address of extremal points emerges as the central idea.
 Lévy C Curve |  Twindragon |  Sink singularities (below) |  Predictive |
9. On the Geometry of IFS Fractals and its Applications
- 2013, PhD Thesis, University of Waterloo (defended on Dec. 17).
- The thesis revolves around the central problem of determining bounding sets to IFS fractals - and the convex hull in particular - emphasizing the fundamental role of such sets in their geometry. This emphasis is supported throughout the thesis, from real-life and theoretical applications to numerical algorithms crucially dependent on bounding.
8. Fractal Potential Flows: An Idealized Model for Fully Developed Turbulence
- Originally titled "Fractal Potential Flows as an Exact Model for Fully Developed Turbulence".
- This paper presents the mathematical model of fractal potential flows, and links it philosophically to the phenomenon of turbulence, building on experimental observations. The model hinges on the recursive iteration of a fluid dynamical transfer operator. We show the existence of a unique attractor in an appropriate space, which will pose as our model for the fully developed turbulent flow field. Its singularities are shown to form an IFS fractal. Meanwhile we present an isometric isomorphism between flows and probability measures, hinting at a wealth of future research.

7. On Intersecting IFS Fractals with Lines
- 2014, Fractals, Vol. 22, No. 4, 1450014.
- Originally titled "On the Intersection of Lines and IFS Fractals".
- The resolution of the Fractal-Line Intersection Problem is imperative for a more efficient treatment of applications, ranging from computer graphics to antenna design. We provide a verifiable condition guaranteeing intersection with any line passing through the convex hull of an IFS fractal. The condition also implies a constructive algorithm for finding the points of intersection. In our effort to quantify intersection, we provide an explicit formula for the well-known invariant measure of IFS.

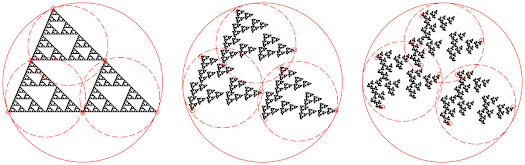
6. Apollonian Circumcircles of IFS Fractals
- 2016, Forum Geometricorum, Vol. 16, pgs. 323–329.
- Originally titled "Explicit Bounding Circles for IFS Fractals".
- Computer-generated plants are often modeled using IFS fractals, and thus their extent in virtual space is a fundamental question, whether for collision detection or ray tracing. We hereby introduce explicit formulas for bounding circles and spheres, providing readily applicable bounding sets for IFS fractals.
Other Papers
5. Geodesics of the Structural Similarity Index
- 2012, Applied Mathematics Letters, Vol. 25, pgs. 1921–1925.
- We construct metrics from the geodesics of the Structural Similarity index, an image quality assessment measure. An analytical solution is given for the simple case of zero stability constants, and the general solution involving the numerical solution of a non-linear equation is also found.
4. On Composite Moduli from the Viewpoint of Idempotent Numbers
- 2004, MSc Thesis, Eötvös Loránd University.
- The thesis introduces novel concepts for the examination of composite moduli, while avoiding the notoriously difficult problem of prime-factorization. Among many interesting new results, it gives generalizations of well-known theorems and definitions, such as the Euler-Fermat Theorem, the concept of primitive roots, and the solvability of binomial congruences.
3. A Generalization of Euler's Criterion to Composite Moduli
- 2016, Notes on Number Theory and Discrete Mathematics, Vol. 22, No. 3, pgs. 9-19.
- 2003, peer-reviewed and presented at the Scientific Student Conference at Eötvös Loránd University.
- Originally titled "Idempotent Numbers and the Solvability of xk ≡ a (mod m)".
- The paper provides a necessary and sufficient condition for the solvability of this equation, where m is any integer, which does not require the prime factorization of m.
2. Solution of a Simple Case of the Navier-Stokes Equations via Employing the Lambert W Function
- 2003, peer-reviewed and presented at the Scientific Student Conference at Eötvös Loránd University.
- The purpose of this paper is to introduce a bivariate function using the Lambert W function, which can be generalized to satisfy Euler’s Equation of Inviscid Motion over a certain domain, with pressure independent of space variables.
1. Limits and Mean Value Theorems for Real-Valued Functions in Hilbert Spaces
- 2002, unpublished.
- The goal of this paper was to prove a theorem which generalizes L'Hôpital's Rule, while giving generalizations for Rolle’s Theorem as well as some mean-value theorems for functions over Hilbert Spaces.